Meta-Query-Net: Resolving Purity-InformativenessDilemma in Open-set Active Learning 논문 공부

이 논문은 NeurIPS'22에 publish된 논문으로 2024.04.09 기준 11회의 citation을 보유하고 있다.

이 논문은 Open-set Active Learning (unlabeled data에 unseen class가 존재) 를 위해 Meta-learning을 적용한 알고리즘으로, open-set AL에서 중요한 두 개념인 purity와 informativeness사이 balance를 맞출 수 있도록 Meta-Query-Net(MQNet)을 제안한다. MQNet은 각 sample에 대해 dynamic하게 최적의 balancing factor를 찾아준다고 한다. 추가적으로, 기존의 Meta-learning literature가 validation set을 query set을 사용하여 meta-learning을 수행했었던 점을 고려했을때, AL 세팅에 맞추어 별다른 validation set의 사용없이 meta-learning을 수행했다는 contribution 또한 존재한다. 이 논문은 https://proceedings.neurips.cc/paper_files/paper/2022/hash/cba6f4460a1f395f68a88598c86e79bd-Abstract-Conference.html 에서 찾아볼 수 있고, 코드는 https://github.com/kaist-dmlab/MQNet.에 있다. 😉

Introduction

◻ 기존의 AL은 대부분 unlabeled data가 모두 in-distribution에 속한다는 unrealistic한 가정을 함

👉 이 논문은 unlabeled data가 out-of-distribution(OOD)에 속할 수 있는 open-set AL을 다룸

◻ 기존의 AL온 보통 uncertainty가 높거나 diversity를 높일 수 있는 샘플을 선택하는 경향이 많음

👉 이 방법은 (쓸모없는) OOD data를 선호하게 만들어 새로운 접근법이 필요함

H : High, L : Low, P : Purity, I : Informativeness

◻ 용어 정리

    ◽ purity : 특정 unlabeled data가 얼마나 in-distribution에 속하는가?

    ◽ informativeness : 특정 unlabeled data가 얼마나 학습 정보량(난이도)가 높은가?

◻ purity-informativeness dilemma (그림(a,b,c)) 

    ◽ HP-HI 샘플을 뽑아야하고, LP-LI 샘플을 뽑지 말아야하는 것은 명확하다

   🤔 그럼 HP-LI, LP-HI 샘플중에는 뭘 뽑아야하는걸까?

        👉 학습 초기에는 purity가, 학습 후기에는 informativeness가 중요하다.

◻ Meta-Query-Net(MQNet) : 두 factor 사이 best balancing을 찾아주는 역할을 한다

    ◽ MQNet을 훈련하기 위해 필요한 data는 selection으로 얻은 데이터(+기존 데이터)를 사용한다.

    ◽ skyline query를 사용해서 MQNet을 더 효과적으로 학습시켰다고 한다

Purity-Informativeness Dilemma in Open-set Active Learning

Problem Statement. 기본적으로 classic AL처럼 여러 round로 구성되어 있고, query & annotate를 반복한다.

◻ 다만, unlabeled에 쓸모없는 OOD data들이 섞여있다.

    ◽ initial labeled set에도 OOD data가 들어있다.

    ◽ OOD data가 select되면 annotate하지 않는듯 하다 (확인 필요)

Purity-Informativeness Dilemma. 

◻ purity-informativeness dilemma : purity & informativeness 둘다 높은 샘플을 선택해야한다.

    ◽ 위 두 factor는 보통 반비례 관계에 있다. (e.g, outlier는 purity는 낮고, informativeneess는 높다)

◻ Meta-task 정의 : <purity, informativeness> 두 값을 input으로 받아 overall score을 예측하자!!

    ◽ main task와 분리되는 meta-task을 똑똑하게 잘 정의하였다!

Meta-Query-Net (MQNet)

◻ 위의 meta-task를 통해 meta-score를 잘 예측하는 MQNet을 세롭게 제안함

    ◽ purity, informativeness 두 factor를 잘 balance하는 역할을 수행함

    ◽ 여타 다른 Meta-learning works처럼 MQNet은 굉장히 작아서 training / infrerence에 무리가 없다

    ◽ self-validation set(이후 설명 나옴)을 사용해서 MQNet을 학습한다고 한다

Training Objective with Self-validation set. 

◻ MQNet은 자체적으로 생산한 self-validation set을 사용하여 supervised manner로 학습된다.

   ◽ 이 self-validation set은 AL의 selection & annotation이후 획득한 ID & OOD data를 의미한다

       ◽ 더 정확히는 아래 Algorithm과 같이 새롭게 selection한 데이터 + 기존의 labeled data 이다.

      👉 이를 통해 추가적인 validation set을 확보할 필요 없이 meta-learning이 가능하다 (호오..🙄)

😉 MQ-Net은 어떻게 동작해야할까?,, meta-objective는 다음의 두 조건을 만족해야한다.

    ◽ 쉽거나 OOD sample에 대해서는 낮은 정보량 $\Phi$ 을 예측해야한다.

    ◽ 어렵운 ID sample에 대해서는 높은 정보량 $\Phi$ 을 예측해야한다.

😵 그럼 이 복잡한 조건을 갖춘 loss를 어떻게 하나의 식으로 압축할 수 있을까?

    ◽ 우선 masked CE loss를 정의한다. 이는 OOD는 0, ID는 CE loss값을 리턴한다. 

masked CE loss

    ◽ 그다음 Hinge loss형태의 objective를 사용한다. 😀👍 

proposed meta-objective

    ◽ Sign 함수는 왼쪽 값이 크면 1, 같으면 0, 작으면 -1를 리턴한다.

    ◽ Constant margin $\eta$는 조금 더 넉넉한 경우에도 loss값이 살아있도록 도와준다.

◻ 이 meta-objective는 다음의 성질을 가진다. (중요!!)

    ◽ $l_{mce}(x_i)$ < $l_{mce}(x_j)$ : $x_i$가 쉽거나 OOD sample 일때 ($x_j$는 어렵거나 ID sample)

       👉 $\Phi_i$는 줄이고, $\Phi$는 키우고..!!

    ◽ $l_{mce}(x_i)$ > $l_{mce}(x_j)$ : $x_i$가 어려운 ID sample 일때 ($x_j$는 쉽거나 OOD sample)

       👉 $\Phi_i$는 키우고, $\Phi$는 줄이고..!!

◻ 이때, s.t. 로 어떤 조건이 하나 달린 것을 확인할 수 있는데 이게 skyline constraints이다!

Skyline constraint

    ◽ skyline constraints는 (확실하진 않으나) 모든 조건을 동시에 만족해야하는 조건인 듯 하다...

       👉 Purity와 Informativeness 대소관계가 MQ-Net에 반드시 반영되야한다!!

    ◽ Purity, informativeness score는 기존의 AL 방법을 그대로 적용해서 구한다.

    ◽ 나중에 ablation study에서도 나오지만, 이 constraint 적용 유무가 성능에 매우 큰 영향을 미친다.

Architecture of MQ-Net

◻ MQ-Net은 자체적으로 두개의 MLP와 간단한 activation으로 구성된다.

◻ MQ-Net은 앞서 나온 skyline constraitns를 만족한다. 

   👉 이 조건을 만족하기 위해 MQ-Net의 모든 parameter는 non-negative 하다.

◻ MQ-Net은 purity score와 informativeness score를 input으로 받는다.

   👉 이 두값은 exponential, normalization 등을 거쳐 일정한 분포의 양수값으로 고정된다.

   

 

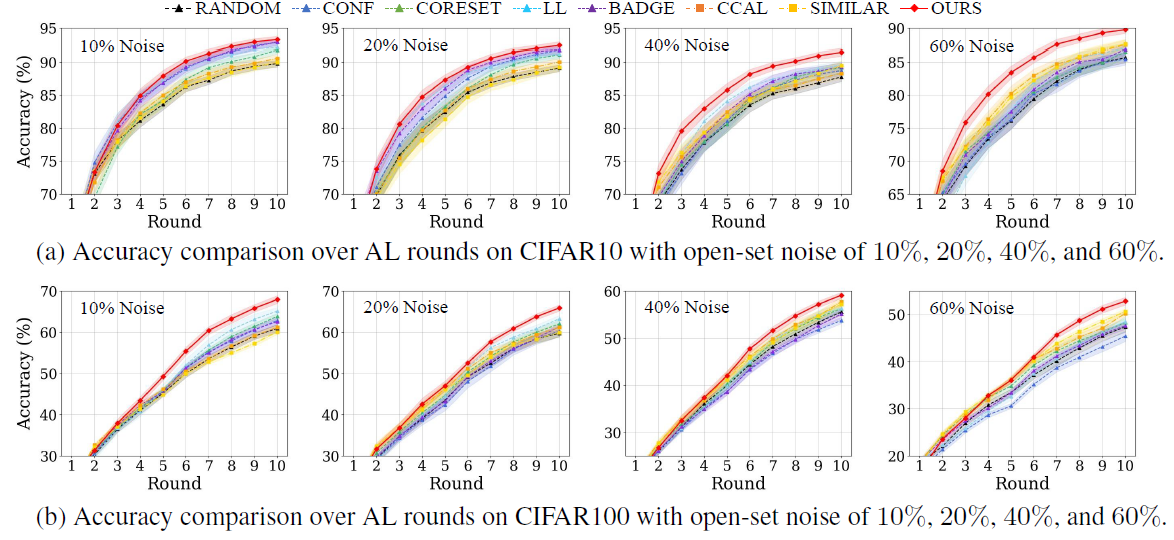
다양한 open-set AL 상황에서 비교군 알고리즘보다 높은 성능을 보였다고 한다~~