이 논문은 CVPR 2020에 publish 된 논문이며, 2023-10-16 기준 인용수 375를 기록중인 핫한 논문이다.
https://bit.ly/motsolv. 에 친절히 코드도 공유되어있다.
Introduction
이 논문이 나오던 시절에.. 대부분의 MOT는 tracking-by-detection으로 해결하는 것이 대세였다. 😉
- frame 별로 object detection을 구한다음,
- 별도의 optimization problem을 풀어서 data association을 수행하는 경우가 많았다.
Data association 문제는 대게 graph partitioning 문제로 모델링되는 경우가 많았는데, node는 object detection으로, edge는 각각의 detection들이 같은 trajectory에 속하는지를 의미하도록 정의하고 Hungarian method등을 적용하고는 했다.
이러한 맥락에서 기존의 MOT 논문들은 주로 아래 두가지 방향으로 연구를 진행시켰는데
- Graph formulation : 여러가지 정보를 융합하여 graph optimization frameworks를 발전시키는 방향
- Learning better cost : DNN 으로 얻은 feature를 사용하여 pairwise cost function을 정의하는 방향
이 논문은 위의 두 방향 융합시킨 learning-based solver 을 제안한다. 기존 work 처럼 cost function을 정의하고 graph optimization 문제를 푸는 대신 neural network을 통해 (구체적으로는 graph structure의 message passing을 통해,, 하지만 graph neural network을 사용하는 것은 아니다) 한번에 graph partitioning (trajectory identification) 을 수행한다고 한다.
❗❕ 기존에 이것저것 지저분하게 heuristics을 적용하던것을 깔끔하게 Message Passing Network (MPN) 하나로 간단하게 만들고, 성능도 SoTA를 찍은데다가, 처리속도도 엄청 끌어올려서 여러 의미가 있는 literature 이라 할 수 있겠다.😉👍
Tracking as a Graph Problem
제시된 알고리즘 framework는 기존 MOT 문제의 network flow formulation을 따른다고 한다.
그렇다면 network flow formulation이 무엇이냐? MOT 조건이 달린 constrained cost minimization (in graph) 세팅을 말한다.
이 constrained optimization 문제에 달린 조건들은 아래와 같다
조건 1 : graph는 binary edge를 가진다. (같은 trajectory면 1, 아니면 0)

조건 2 : 각각의 node (object detection)은 미래/과거 각각에 대해 단 하나의 node와만 연결될 수 있다.

Optimization : 이 formulation은 각각의 edge $y_{(i,j)}$에 대응되는 cost $c_{(i,j)}$의 합을 최소로 만드는 minimization 문제.

이 논문에서 제안되는 모든 알고리즘은 위 optimization 문제를 해결하기 위함이고, 이에 더해 network flow formulation의 고유한 constraints로부터 inductive bias를 얻어 알고리즘에 여러 부분을 추가적으로 개선하였다. 😉
Learning to Track with Message Passing Networks
이 work의 main contribution은 MOT tracker를 미분가능한 edge classifier framework로 모델링했다는 것이다.
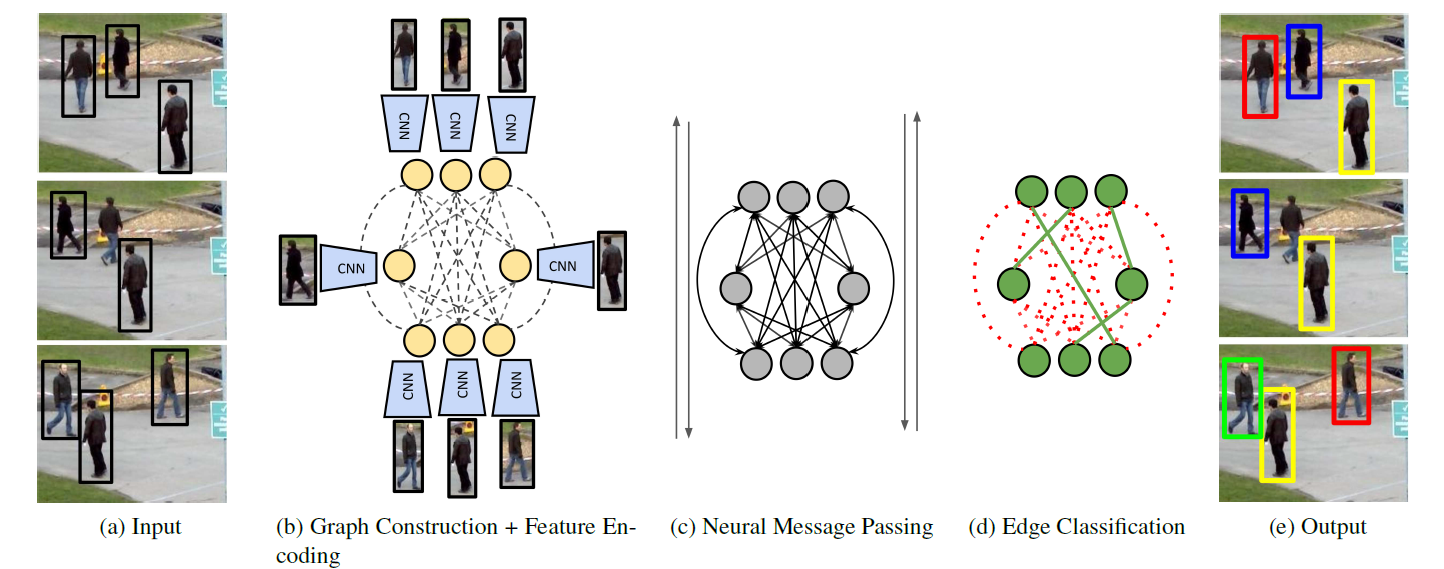
제안된 알고리즘 pipeline은 아래 4개의 main stages를 거쳐 동작한다. (위의 Figure 참고)
[1] Graph Construction : set of object detections이 input으로 주어졌을때, 위 figure의 (b) 처럼 graph 구조를 구축한다.
(node는 CNN을 통해 계산된 appearance embedding을 사용한다. edge는 MLP에다 apperance embedding이랑 여러 localization 정보 (높이, 이전 object와의 거리/시간차) 를 통과시켜 encoding 된 feature vector를 사용한다.)
[2] Neural Message Passing : Message Passing Network (MPN)을 사용해서 node/edge 에 저장된 정보들이 이웃으로 점점 뻗어나가며 high-order information을 교환한다.
[3] Training : Message passing이 끝난 feature로 예측한 final detection의 category/localization/ID 를 supervise한다.
* test 시에는 edge 에 대한 prediction에 rounding 및 maximum 연산을 통해서 ID 정보를 구한다고 한다.
Message Passing Network
맨처음 논문을 읽었을때는 graph neural network (GNN) 을 통해서 문제를 해결하는 줄 알았다. 그런데 계속 읽어보니 GNN이 아니라 graph 적용할 수 있는 CNN/MLP를 사용했다고 보는게 맞는 것 같다.
(GNN은 edge에 대응되는 feature가 없고, node feature update할때 incouming/outcoming node+edge 를 전부 concat해서 module에 통과시킨다거나 하는 행동은 하지 않는다.)
(나도 읽어보진 않았지만, 이 "message passing step"이라는 propagation procedure는 "Neural relational inference for interacting systems" 같은 논문에서 이미 많이 다뤄진듯하다.)
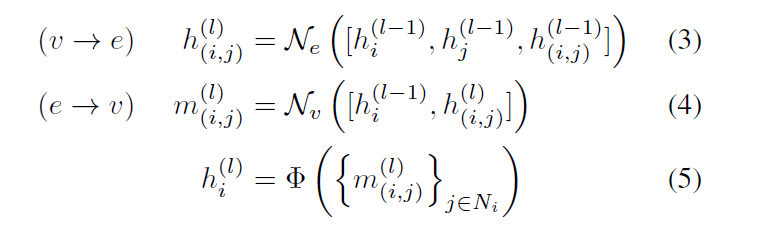
여기서 $N_e$, $N_v$ 이 MPN을 말하는 건데, 각각 edge와 vertex에 대응되는 neural network이다.
edge/node의 feature를 업데이트 할때 주변 정보들을 concat 한다음 MPN에 통과시킨 값으로 간단하게 업데이트한다.
$\Phi$는 order-invariant operation (e.g., summation, maximum, average)이고, $l=1,2,...,L$ 은 interation number.
일반적인 GNN과 같이 L 값이 커질수록 CNN처럼 receptive field가 커지는 것이고 더 멀리 메시지가 전파된다.
Time-Aware Message Passing
위에서 보았던 network flow formulation을 기억하는가? MOT의 graph는 여러 조건이 달려있고, 논문의 저자는 이 조건들로부터 inductive bias를 얻어 Message passing procedure를 더 효과적으로 개선하였다.

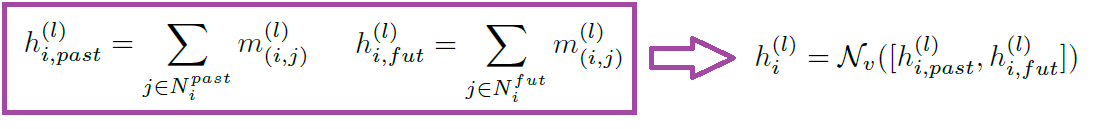
"Time-aware" message passing이 무엇인지 한줄로 설명하자면 : 과거 frame과 미래 frame을 따로 처리한다음 합치자!
원래는 vanilla message passing은 위 figure의 (b) 처럼 모든 incoming/outgoing node와의 연산결과를 한번에 더해서 node feature를 updage하는게 일반적이지만, Time-aware node update에서는 과거와 미래를 따로 연산한다음 이를 concat 해서 별도의 module 에 통과시킨 값으로 node를 update한다.

Feature encoding
node embedding과 edge embedding을 어떻게 초기화하는지에 대한 내용이다.
Node embedding : appearance embedding이다. 각 object detection에 대응되는 영역을 별도의 encoder module $N_v^{env}$ 에 통과시킨 값으로 node embedding을 초기화한다.
Edge embedding : geometry embedding을 사용한다. 아래와 같이 두 node (object detection) 의 box의 좌표 차이, 가로세로 길이 차이, time difference, appearance embedding 차이를 concat해서 $N_e^{env}$ 통과시킨 값을 사용한다.
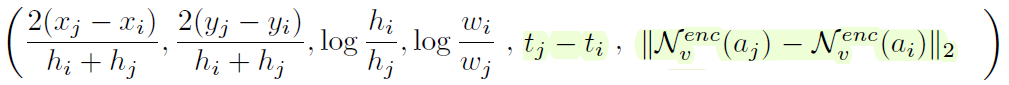
Training Loss
흠.. 논문에는 MPN을 학습하는 loss 밖에 나와있지 않다. 🤔 코드를 봐야겠지만 detector는 별도로 학습하나 싶다.
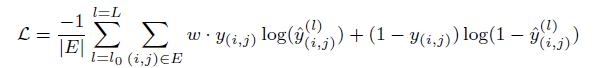
MPN은 위와 같이 binary cross entropy를 사용한다 (MPN의 edge module이 binary classification을 수행하니까).
실제로는 edge 의 value가 1보다 0이 훨씬 많기 때문에 imbalance를 해결해주기 위해 weight $w$ 로 균형을 맞춘다.
Implementation Details
- Backbone으로는 ImageNet에서 학습된 ResNet50을 사용했다.
- Market1501, CUHK03, DukeMTMC 데이터셋을 사용했다.
- 8 graph를 하나의 batch로 묶어 사용했고, 각각의 graph는 6 frames 간격으로 떨어진 15 frames 으로 구성된다.
- ResNet 을 추가로 학습하는건 큰 성능 향상이 없어서 freeze 하고 나머지만 학습했다고 한다.



