이 논문은 CVPR'23에 publish된 논문으로 2023.12.21 기준 12회의 citation을 보유하고 있다.
이전에 리뷰했던 논문 CoTTA나 ECoTTA 처럼 continual TTA 를 다루는 논문인데,, source domain에 pretrain된 model이 15개 정도의 target domain (e.g., corruption) 에 순차적으로 adapt하며 매 domain을 거칠때마다 성능을 측정한다. 언제 새로운 target domain으로 전환되는지에 대한 줄 수 없기 때문에 빠르게 적응할 수 있고, catastrophic forgetting에 강인한 TTA 논문을 개발하는 것이 중요하다. 이 논문은 https://arxiv.org/abs/2212.09713 에서 찾아볼 수 있고, 코드는 https://github.com/dhanajitb/petal 에 있다. 😉
Introduction
먼저, 이 논문은 기존 대부분의 TTA 논문이 non-stationary Continual TTA 를 고려하지 않는다고 비판한다.
(사실 Continual TTA 는 CoTTA에서 이미 제안했고, 똑같이 비판한 부분이라 크게 novel하게 느껴지지는 않았다. 🤔)
여기서 Continual TTA란 test-time 에서 model도 모르는 사이에 domain의 종류가 계속 바뀌는 경우인데, 예를 들어 자율주행중에 날씨가 "화창 $\rightarrow$ 흐림 $\rightarrow$ 비 $\rightarrow$ 눈 $\rightarrow$ 밤" 처럼 계속 변하는 상황을 고려할 수 있다. 이런 Continual TTA 상황에서 model은 긴~~시간 동안 다양한 domain을 거치기 때문에 기존의 TTA works에서 다음의 문제들이 발생할 수 있다.
(1) Error accumulation : 많은 TTA methods 가 pseudo-label 기반의 self-training 이므로 긴 시간동안 error가 누적된다.
(2) Catastrophic forgetting : 긴 adaptation 을 거치면서 source domain의 정보를 잊게된다.
(3) Miscalibrated predictions : 상기 overfitting 등의 이유로 overconfident prediction을 하게된다.

이 단점들을 극복하고자 저자들은 Probabilistic lifElong Test-time Adaptation with seLf-training prior (PETAL) 을 제안하였다.. 이 알고리즘의 특징은 아래와 같다.
(1) 확률 기반의 TTA 알고리즘 (MAP method) 를 제안하였다.
(2) Student model의 moving average로 teacher model을 정의하였다.
Teacher model로부터 pseudo-label을 생성하여 student model으로 cross-entropy loss를 정의하였다.
(3) Fisher Information Matrix 기반 (data-driven) parameter restoration 기법을 제안하였다.
Method : Probablistic Framework for TTA
Bayesian Supervised Learning. Bayesian learning의 목적은 주어진 dataset $D$와 model prior $p(\theta)$를 가정했을때, model posterior $p(\theta|D)$를 찾는 것이다. 👉 이후 Bayesian Inference를 통해 임의의 x에 prediction을 할 수 있다.
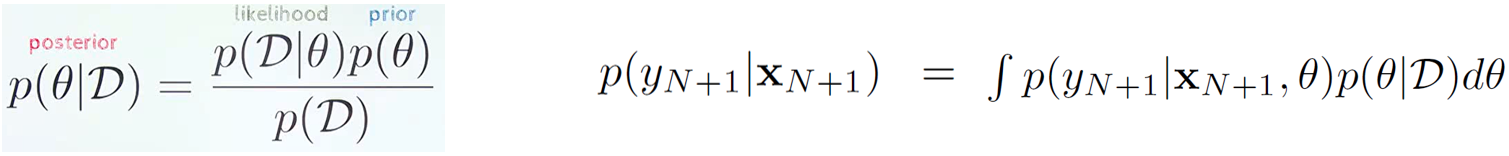
Bayesian Semi-Supervised Learning. Generative model $\psi$로부터 unlabeled data $\{x_m\}_{m=1}^M$이 생성된다고 가정해보자. 이 경우, label을 사용해서 model parameter $\theta$를 추론할 수는 없지만,, data-dependent prior를 구할 수는 있다. 굉장히 posterior처럼 생겼지만, 아무튼 prior라고 한다. (말장난 같음🤔)
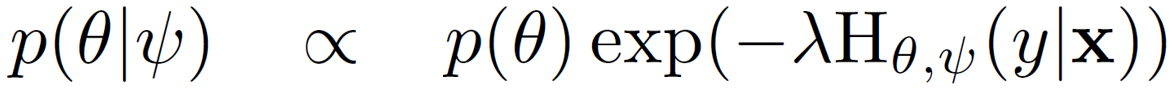
Bayesian Semi-Supervised Learning with Self-Training. 간단히 말해서, 위 Shannon-Entropy $H$ 대신, (student model과 teacher model 사이의) Cross-Entropy $H^{xe}$를 사용한다. 어떻게 cross-entropy가 shannon-entropy를 대체할 수 있는지는 모르겠지만,,, 별다른 설명 없이 이 method를 제안하였다.. 🤔🤔.
👉 Student model의 output $y$, teacher model의 output $y'$이 있을때, MAP objective는 아래와 같이 정의된다.

Bayesian Semi-Supervised Learning with Unlabeled Data Distribution Shift. Source domain의 generative paramter $\psi$ 이외에 target domain의 generative parameter $\bar{\psi}$가 있다고 생각해보자. 그 경우, data-dependent prior는 $\psi$와 $\bar{\psi}$에 대한 scaler를 단순히 곱해주는 것으로 정의될 수 있다고 한다. (왜인지는 모르겠다 🤦♂️🤦♂️)
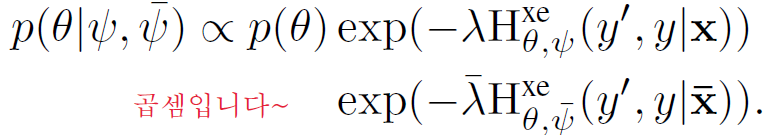
위 prior의 data distribution $p(x|\psi), p(\bar{x}|\bar{\psi})$를 empirical distribution으로 대체하면 다음과 같다.
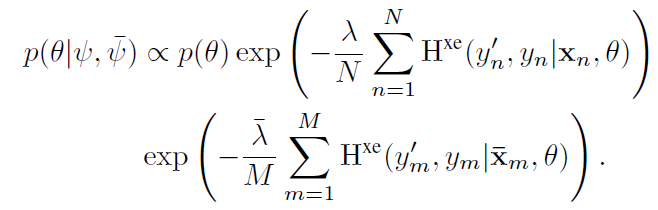
이제 남은건 위에 있는 posterior를 maximize 해서 (MAP) 최적의 conditional parameter distribution을 찾는 것이다. 위 posterior 식에서 양쪽에 log를 취하면 다음과 같다.

여기서 두가지 trick이 추가로 들어가는데
(1) $log p(\theta) + \sum_{n=1}^N log p(y_n|x_n,\theta)$ 에 대해 이미 MAP를 끝마친 결과가 source model (pre-trained model $q(\theta)$) 이므로 상기 term을 그냥 $q(\theta)로 대체할 수 있다.
(2) 이미 likelihood $p(y|x,\theta)$를 계산할 때 labeled data ($x_n, y_n$)을 사용했으므로, labeled data의 cross entropy $H^{xe}(y',y|x)$는 무시할 수 있다. (음.. 이게 왜 가능한거지? 🤦♂️🤔🤦♂️🤔)
하여튼간에 최종적인 MAP objective는 다음과 같다.
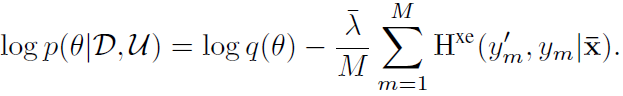
❗😣 $log q(\theta)$를 어떻게 계산하느냐가 문제인데, SWAG-Diagonal이라는 방법을 사용한다고 한다. 근데 문제는 pretrained model도 이 방법으로 학습된 Bayesian neural network이어야한다는 점..
Method : Parameter Restoration
Stochastic Restoration.이건 CoTTA에서도,,, 그리고 이전의 continual learning work에서도 많이 사용하는 방법인데,, adapted model $\theta_{t+1}$의 일부 parameter를 확률적으로 pretrained model $\theta_0$으로 되돌리는 방법이다. 이때, CoTTA는 모든 parameter에 동등한 확률을 적용하여 restoration을 수행했지만, PETAL은 Fisher Information Matrix (FIM)을 사용하여 중요도가 낮은 parameter만 restore 한다.


아래 최종적인 algorithm을 첨부하였으니 참고하시라
❗😣 근데 PETAL의 가장 큰 단점은 Bayesian 방법론으로 학습한 pretrained model이 필요하다는 것이다.

Experimental Reseults
대체로 성능 향상은 상당히 실망스럽다. 성능으로 붙은 논문은 아닌 것 같다.
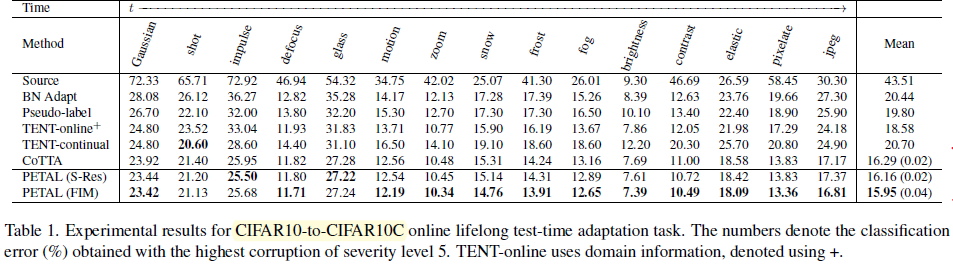
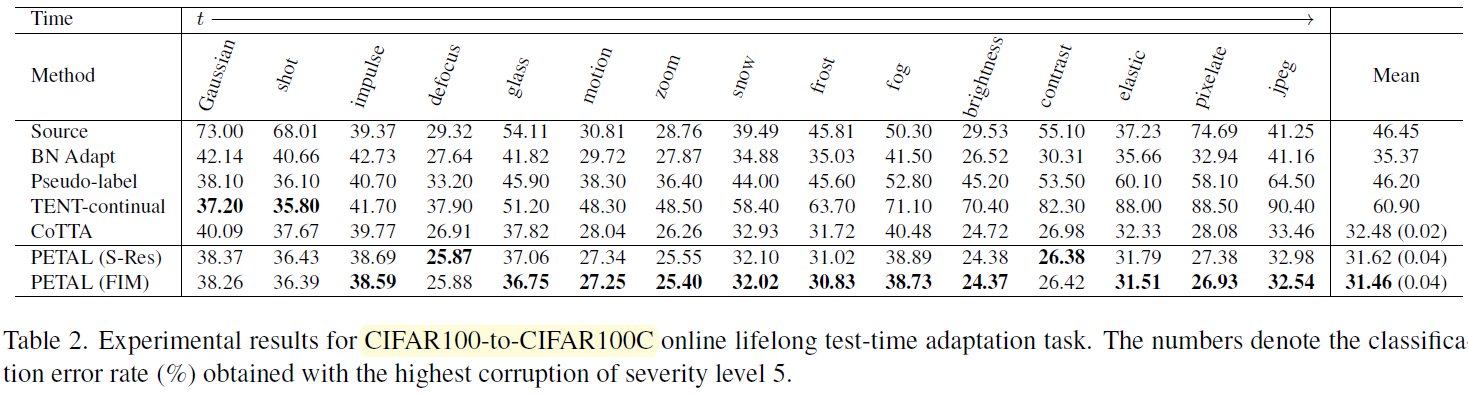
이상 끝! 💪😀🤜



